Diffusion

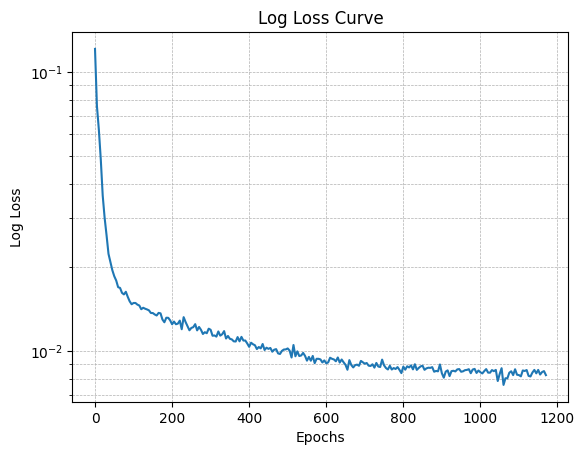
Part 0: Setup

In this project, we use the DeepFloyd IF diffusion model, a two stage model trained by Stability AI.
The first stage takes in a text prompt, and outputs a 64x64 image. The second stage takes in a 64x64 stage and upsamples it to 256x256.
The main parameter that can be adjusted is num_inference_steps, which controls how many "denoising steps" to take. The high level summary is that a diffusion model is trained to remove noise from an image, and it "generates" novel images by taking some number of denoising steps on complete noise. (You can think of noise for images as more and more grainy images). More steps means higher quality, but more computation time.
Below, you can see three different prompts to the diffusion model, in increasing number of denoising steps.
We use seed=18010 (which is also used for the rest of the project).

Part 1: Sampling Loops

In the next few parts, we sample the DeepFloyd denoiser model for different applications.

1.1 Forward Process

As discussed earlier, diffusion models are trained to remove noise from an image. An important part of diffusion is adding noise. The forward process can be described by:
\( \begin{equation} x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1 - \bar{\alpha_t}}\epsilon \end{equation} \)
Where \( \epsilon \sim N(0, 1) \), and \( \bar{\alpha}_t \) are hyperparameters that control the variance and mean over time. In this project, we use DeepFloyd's hyperparams.
Below, a visual example of the forward noise is shown.

1.2 Classical Denoising

Classical denoising uses blurring, applying a low frequency filter, typically Gaussian. Noise is usually some high frequency perturbations that we hope blurring will remove. This doesn't work well with higher levels of noise. Below, you can see examples of Gaussian blurring applied until most of the noise is not observable (chosen by manual inspection).

1.3 Implementing One Step Denoising

We can utilize the off-the-shelf DeepFloyd model to remove noise. We can do this denoising with one step, by rearranging the forward process equation:
\( \begin{align} x_t &= \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1 - \bar{\alpha_t}}\epsilon \nonumber \\ \sqrt{\bar{\alpha_t}}x_0 & = x_t - \sqrt{1 - \bar{\alpha_t}}\epsilon \nonumber \\ x_0' &= \frac{x_t - \sqrt{1 - \bar{\alpha_t}} * \tilde{\epsilon}}{\sqrt{\bar{\alpha_t}}} \end{align} \)
Where, in equation (2), we use \( \tilde{\epsilon} \) to show that we are using the model's estimate of the noise, and \(x_0' \) to show that this is an estimate of the clean image.
Our belief of the "clean image" is an estimate of the image at time 0 in a forward noise process.
Notice in the images below that you can hardly see anything!

1.4 Iterative Denoising

Diffusion models are trained to denoise step by step. In practice, this is expensive; if our goal is to take 1000 steps of denoising from pure noise, then we would have to run the model 1000 times (each step time conditioned). Instead, we can take strided steps; here we start from 990, and take strided steps of 30. The formula to do strided steps is given as: \( \begin{equation} x_{t'} = \frac{\sqrt{\bar{\alpha}_{t'}}\beta_t}{1 - \bar{\alpha}_t} x_0 + \frac{\sqrt{\alpha_t}(1 - \bar{\alpha}_{t'})}{1 - \bar{\alpha}_t} x_t + v_\sigma \end{equation} \) Where here \( x_{t'}, x_t \) denote the denoised image at times \( t' < t \), \( \bar{\alpha}_t \) are DeepFloyd's hyperparameters that control the noise per timestep, \( \alpha_t = \frac{\bar{\alpha}_t}{\bar{\alpha}_{t'}}, \ \beta_t = 1 - \alpha_t \), and \( x_0 \) is our estimate of the clean image at time zero according to equation (2) from the one-step denoising. \( v_\sigma \) represents random noise or variance; DeepFloyd's diffusion model also predicts this as one of its outputs.
This equation can be interpeted as linear interpolation or a Bellmen-esque learning of what \( x_0 \) should be.
Every timestep, we replace a portion of our current state or belief (the noisy image) with our prediction of the clean image.
Note that this process is ultimately probabilistic; below, you can see the iterative process of denoising for one sample of the model, but you can also see another finished sample as well. Notice how the end image's realism is quite good, but only the big ideas or largest features are kept (a white tower, landscape), but the minute details are lost. This is expected because of how much information is lost to the noise. We can see that it is much better than our previous denoising strategies with the one-step and Gaussian methods.

1.5 Diffusion Model Sampling

Now, instead of generating a noisy image from a real image, we can just give the diffusion model complete noise and see what it generates. We prompt the model with "a high quality photo" to get slightly better results. However, without additional tricks, the diffusion model does not have great results. Below, we showcase 5 samples, generated from denoising completely random noise. Both the 64x64 sample is shown and the upsampled 256x256 version using the second stage of the DeepFloyd model.

1.6 Classifier Free Guidance

One trick that has been discovered to improve diffusion model generation is classifier free guidance. The idea is that you can run noise estimates from the model that are conditioned and unconditioned. For example, our conditioned prompt above was "a high quality photo"; but you could also prompt with nothing: "", and get an unconditioned noise estimate from the model. Classifier free guidance works by implementing a modified noise estimate: \( \begin{equation} \epsilon = \epsilon_{u} + \gamma(\epsilon_{c} - \epsilon_{u}) \end{equation} \) Where subscript c denotes conditioned, and u denotes unconditioned. For \( \gamma = 0\), we recover the conditional noise estimate, and for \( \gamma = 1 \), we get an unconditional noise estimate. CFG works by setting \( \gamma > 1 \); why this works is currently up to debate.
Personally, one way to interpret it is that by subtracting a large amount of unconditioned noise, you are amplifying the conditioning signal. Just as LLMs seem to encode data in a vector space, perhaps the noise also exists as a multidimensional vector. Then the difference of the unconditioned noise and the conditioned noise represents the direction that encodes just the prompt's influence.
(This is like the discovering that the embedding of 'king' - 'man' + 'woman' = 'queen'; here, 'conditioned' - 'unconditioned' = 'high quality photo',
with implied 'conditioned' = 'some_base_noise' + 'high quality photo').
Here, we use \( \gamma = 7 \); the noise estimate equals \( \epsilon_u + 7\epsilon_{\text{diff}} \).
The results are better than above; the fifth sample in particular looks quite realistic.

1.7 Image-to-image Translation

Now we apply CFG generation to a slightly noised image, and then see what happens to it. We show decreasing amounts of noise added, using i_start = [1, 3, 5, 7, 10, 20] . Larger i_start corresponds with less noise and less strided steps. In the examples below, you can see that the earier steps are random generations, because there is too much noise. This algorithm is called SDEdit.

1.7.1 Hand-Drawn, the Web

SDEdit can also be applied to hand-drawn photos to "realize" them as realistic images. Here are some examples.

1.7.2 Inpainting

In a similar vein, we can use diffusion to only re-generate parts of an image. This is done by allowing the model to predict noise for an entire image, and only using its noise estimate to update a portion of the image according to a mask. The rest of the image is treated differently, and noised by the forward process instead (ie. we start with a noisy version of our ground truth, we allow the model to de-noise part of the image, then noise the ground truth image to a smaller timestep \( t' < t \) and apply the iterative de-noising on the masked region only).
Below, we show some results.

For the Campanile, the diffusion model generates a new lighthouse-esque top.

For the cat, the diffusion model decides to replace the head with a baby's head. This is a pretty out-of-place generation, but we have to keep in mind that this is a novel non-training task for the DeepFloyd model. The noisy starting point most likely allowed the model to be "creative" by itself for too long, without a clear context of a cat.

For the dog, we use a different type of mask; kind of a "outpaint", where the model is allowed to draw around the head of the dog. Here, it also seems likely that the model generates without much context of the dog early on, creating a woman's face around the dog's face. Interestingly it does seem to give the dog a bit of a bordered window, and the window does not map completely with the mask; notice on the left side the dog area pokes out.

1.7.3 Text-conditional Image-to-image Translation

The SDEdit algorithm (take an image, add noise, "project" to the image manifold via diffusion) can also be used with a different prompt in the projection step. This provides some guidance on how the model should re-generate or edit the image. Below, we show image-to-image translations, using the prompt 'a lithograph of a waterfall' (A lithograph is an art form or printing method, using a plane and certain liquid properties).
Particular interesting generations: Campanile at noise 10, Cat at noise 20, Dog at noise 20.

1.8 Visual Anagrams

Taking diffusion model tricks even farther, we can create visual anagrams with diffusion models. Here, we present images that look like one thing in a certain direction, and another image when flipped upside down! This is done by first by estimating noise while conditioning the model with prompt A, and then flipping the image and acquiring the noise estimate while conditioning the model with prompt B. Averaging the noise estimate A, and the flipped noise estimate B, the image generated with develop along both prompts at the same time. This is described by:
\( \begin{equation} \epsilon = 0.5 (UNet(x_t, t, prompt_A)) + 0.5 flip((UNet(flip(x_t), t, prompt_B))) \end{equation} \)
However, we use CFG for generating \( \epsilon_A, \epsilon_B \). Below, we show pairs of images representing visual anagrams.

1.9 Hybrid Images

Hybrid images look like one thing from up close, and another image from farther away. We can achieve this effect in diffusion by using a similar manipulation to above. Instead of flipping, we apply a low pass or high pass filter to different noise estimates: \( \begin{equation} \epsilon = f_{lowpass} \epsilon_A + f_{highpass} \epsilon_B \end{equation} \)

2 Training UNets for MNIST

In the following parts, we train three different UNets for denoising MNIST images. See CS180 Proj5 Part B spec for an in depth explanation of the simplified UNet architecture.
The first one is unconditioned; we train with noised MNIST images \( \sigma = 0.5 \).
The next is time conditioned. We show samples from this neural net, generated by providing pure noise, and max time.
The last is time and class conditioned. We show samples generated by noise and conditioned on a certain class.

2.1 Unconditioned UNet

The unconditioned net was trained with noised MNIST images \( \sigma = 0.5 \), and trained for 5 epochs using PyTorch's builtin MNIST training dataset.
Below, we show the noising process used for training, the training loss curve, sample denoised images from the test set, and sample out-of-distribution denoised images.

2.2.1 Time Conditioned UNet

For a real diffusion model, we need to condition on time. Here, we elect to learn a time embedding to add to the internal representation of the UNet in the upsampling steps (the right side of the U), on the lower two levels. We use two different fully connected blocks to learn the time embeddings. We run for 20 epochs.
During training, we randomly sample a time \( t \in [0, 300] \) to apply noise according to the forward process equation, and ask the model to denoise it completely. (The loss is mean squared error with the ground truth image).
Note that we still sample the model with the iterative process. These samples are not the best; this is probably because during the sampling process, the model "has no way" to know or "decide" what class it is generating, and runs into some trouble.

2.2.2 Class Conditioned UNet

To improve our time conditioned UNet, we can also condition on class! We use a one-hot vector to encode the class, and learn and inject a class embedding similar to the time embedding. However, we multiply the internal representation with our class embedding, and also train with a chance to drop the conditioning information; \( p_{uncond} = 0.1 \) during training. (The model is forced to generalize its denoising.)
We show examples of all the classes (this time we can ask for specific digits from the model during iterative diffusion sampling!). The results are much better!